Prompted by the final space shuttle launch of Atlantis, I thought I would have another look at two line elements (TLEs). These are coded lines of data that describe the orbital dynamics of a space vehicle. The last time I looked at this was when I was working on a GPS tracking project and we wanted to predict the satellite constellation at a particular time of day, but TLEs can also be downloaded for the shuttle and International Space Station.
NASA’s J-Track shows the shuttle and ISS in near real-time: http://spaceflight.nasa.gov/realdata/tracking/index.html
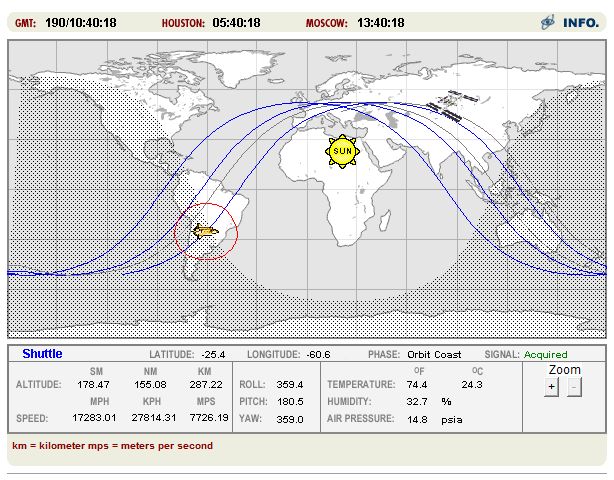
The TLE for the shuttle can be downloaded from the following link:
The mathematics to calculate a position from the TLE is published in the NORAD paper entitled “Spacetrack Report Number 3” (1980/1988). A later revision to this paper is also publicly available and there are various ports of the algorithm from Fortran into C, C++ and C#. While investigating this, I stumbled across a very useful library written by Michael F. Henry. It’s called “OrbitTools” and is a C++ and C# (both managed .net) implementation. His download page contains lots of other useful information and links to the spacetrack revised paper:
http://www.zeptomoby.com/satellites/
The next step was to download his C# library and write the code to load the shuttle TLE and convert the position to a location on the Earth. One point worth mentioning here is that the library calculates lat/lons in WGS72 rather than WGS84. The spheroids are slightly different, so there will be some small accuray issues, but it’s close enough for our purposes.
Having downloaded and included the OrbitTools library into a new C# project, the code to calculate the shuttle position is as follows:
[csharp]
const string TleTitle = "SHUTTLE";
const string Tle1 = "1 37736U 11031A 11190.45039996 .00020000 00000-0 20000-3 0 9019";
const string Tle2 = "2 37736 51.6412 48.9000 0077926 223.8647 135.6325 16.00701051 142";
//DateTime dt = DateTime.UtcNow;
DateTime dt = new DateTime(2011, 7, 9, 10, 40, 18, DateTimeKind.Utc);
Tle VehicleTle = new Tle(TleTitle, Tle1, Tle2);
Orbit VehicleOrbit = new Orbit(VehicleTle);
TimeSpan ts = VehicleOrbit.TPlusEpoch(dt); //how old is our TLE?
Eci VehicleEci = VehicleOrbit.GetPosition(dt); //OK, they want GMT, not UTC
CoordGeo VehicleGeoCoord = VehicleEci.ToGeo();
double lat = VehicleGeoCoord.Latitude*180.0/Math.PI;
double lon = VehicleGeoCoord.Longitude*180.0/Math.PI;
double alt = VehicleGeoCoord.Altitude;
if (lon > 180.0f) lon = -(360.0f – lon);
Console.WriteLine(TleTitle+": lat=" + lat + " lon=" + lon + " alt=" + alt);
[/csharp]
When this is run, the result written to the console is as follows (apologies for the unnecessary precision, but that’s the output I get):
lat=-25.316480642262878 lon=-60.024030447329437 alt=291.32191224312828
These values are very close to the figures on NASA’s J-Track image reproduced earlier, so we’re close to the official coordinates. When repeating this, it’s important to fix the time in the code to the same time as displayed on the J-Track applet and not just use “DateTime.UtcNow” as is commented out in the code. This is one source of inaccuracy as we’re assuming the position was calculated at zero milliseconds, which might not be the case.
References and Links
NASA J-Track: http://spaceflight.nasa.gov/realdata/tracking/index.html
OrbitTools C++/C# SGP4/SDP4 Library and other information: http://www.zeptomoby.com/satellites/
TLE Data for STS 135: http://spaceflight.nasa.gov/realdata/sightings/SSapplications/Post/JavaSSOP/orbit/SHUTTLE/SVPOST.html
Original Spacetrack Report Number 3 (1980): http://www.celestrak.com/NORAD/documentation/spacetrk.pdf
Spacetrack Report Number 3 Revisited: http://www.celestrak.com/publications/AIAA/2006-6753/
Other sources of TLE data: http://celestrak.com/NORAD/elements/
